時系列データに異常発見。「時系列異常検知」とは
2020.10.20
株式会社Laboro.AI リード機械学習エンジニア 大場 孝二
概 要
気温や降水量をはじめとする気象データや交通量データなど、時間の変化に沿ってまとめられた情報は、時系列データと呼ばれます。時系列データは、時期や時間ごとの変化を捉えるため主に用いられますが、ビジネスシーンではこうした時系列情報をただ捉えるだけでなく、急激な変化や異常が起きた場合にそれを察知したり、場合によっては通知するような仕組みを検討することも重要なポイントになるはずです。
このコラムでは、こうした時系列データに表れる異常を検知するための手法「時系列異常検知」の紹介と、とくにSR法と呼ばれる手法の技術解説をしていきます。
目 次
・時系列異常検知とは
・Spectral Residual(SR法)
・SR法の技術概要
・技術解説
・SR法を異常検知に適用する
・論文著者たちの工夫
・SR法のデータへの適用例
・いろいろなデータに対してのSR法の適用
・検知できるケース
・検知できないケース
・その他のケース
・まとめ
・参考文献
時系列異常検知とは
安定していた株価が急変した、動きを保っていた機械が急におかしな動きをしだした、一定量だったSNSの投稿量が激増(炎上していた)など、「いつもと違う」で表されるような急激な変化は、私たちの身の回りでもしばしば発生します。
「時系列異常検知(Time Series Anomaly Detection)」は、その名の通り、時系列上に並べられた大量のデータから、通常とは異なる値や変化、動きを見つけ出す技術です。上の株価データや機械センサーのデータ、SNS投稿のようなトラフィックデータはその代表的な例ですが、データ上に表れる急激な変化を捉えることは、ビジネス上の危機管理や安全管理に結びつく重要な取り組みと言えるでしょう。
今回は、その時系列異常検知の手法の一つである、Spectral Residual(SR法と呼びます)を、その研究論文Time-Series Anomaly Detection Service at Microsoft をベースにしながら紹介したいと思います。また、実際にSR法を用いてデータ分析を行い、どのようなデータだと異常を検知しやすく、また検知しにくいのかということを見ていきます。

Spectral Residual(SR法)
SR法は、実はもともと画像データに対して用いられていた手法です。画像の中にある人が感じる特徴的な箇所、つまり際立った傾向がある部分を捉えるための技術としてSR法が用いられます。(参考文献①)
具体的には、SR法では2次元で表現される画像データをフーリエ空間(周波数に変換・表現した空間)で処理を行うことで、特徴を捉えます。下の図は、入力された画像イメージにSR法を適用したものです。3×3、5×5、7×7、3つのフィルター(local average)の幅での結果を示していますが、いずれでも家のある位置が強調されていることがわかります。

このSR法を時系列データに適用するということは、一次元のデータに適用するということです。先に結果を示すと以下のようになります。2次元の画像データと同じように、1次元の時系列データでも赤点の部分の異常値が強調されていることがわかります。

SR法の技術概要
以下からは、SR法の詳細について、論文”Time-Series Anomaly Detection Service at Microsoft“に基づいて、その技術的な概要を解説していきます。
SR法によって算出される値をsaliency mapと呼びます。SR法による異常検知は、時系列データに対してSR法を適用してsaliency mapを算出、そしてsaliency mapがある閾値以上の点をanomaly(アノマリー:異常値)と判定するものです。
具体的には、時系列データから実空間データをフーリエ空間に飛ばし、フーリエ空間上で“ある処理”をした後に、実空間に逆フーリエ変換で引き戻す手法です。“ある処理”というのは、上で見たように、周りと違う周波数領域を際立たせるというもので、そうすることで実空間での特徴的な部分を際立たせることができると考えられています。
問題設定として一次元データで考えた場合の手順を、次に解説していきます。
技術解説
\(\vec{x}\ =(x_1, x_2, \cdots, x_n)\)を実空間のベクトルとします。これをフーリエ変換することで、\(\vec{f}\ =(f_1, f_2, \cdots, f_n)\)が得られます。それぞれの\(f_j\)は複素数で、\(f_j = r_j \exp(i \theta_j) (r_j, \theta_j \in \mathbb{R})\)と表現します。そして、絶対値成分である\(r_j\)を変換して\(f’_j = r’_j exp(i \theta_j) (r’_j, \theta_j \in \mathbb{R})\)を新たに作成します(\(r’_j\)を算出する式は後述)。\(\vec{f’} \ = (f’_1, f’_2, \cdots, f’_n)\)に対して逆フーリエ変換を行い、実空間に引き戻したベクトル\(\vec{x’} \ = (x’_1, x’_2, \cdots, x’_n)\)に対して絶対値成分を取り出した\(\vec{S} \ = (\|x’_1\|, \|x’_2\|, \cdots, \|x’_n\|)\)をsailency mapと呼びます。saliency map は、上で書いたとおり、\(\vec{x}\)の人間が見て「特徴的だなー」と感じる点を際立たせたものです。ここで、\(\log{r’_j}\)は、\(\log{r_j}\)に対して直近の平均を引いたもので、数式で表現すると、\(\log{r’_j} =\log{r_j} – \frac{1}{q}\sum_{i=1}^{q}{\log{r_{j+1-i}}}\)です。\(q\)はハイパーパラメーターで、local average を算出する際に使用するデータ数です。
この手順をまとめると、次のようになります。
1. フーリエ変換
・ \(\mathcal{F}:\vec{x}\ = (x_1, x_2, \cdots, x_n) \mapsto \vec{f}\ = (f_1, f_2, \cdots, f_n)\)
・ \(f_j = r_j \exp(i \theta_j) (r_j, \theta_j \in \mathbb{R})\)
2. フーリエ空間での処理
・ \(\vec{f}\ = (f_1, f_2, \cdots, f_n) \mapsto \vec{f’}\ = (f’_1, f’_2, \cdots, f’_n)\)
・ \(f’_j = r’_j exp(i \theta_j) (r’_j, \theta_j \in \mathbb{R})\)
・ \(\log{r’_j} =\log{r_j} – \frac{1}{q}\sum_{i=1}^{q}{\log{r_{j+1-i}}}\)
3. 逆フーリエ変換
・ \(\mathcal{F}^{-1}:\vec{f’}\ = (f’_1, f’_2, \cdots, f’_n) \mapsto \vec{x’}\ = (x’_1, x’_2, \cdots, x’_n)\)
・ \(\vec{S}\ = (\|x’_1\|, \|x’_2\|, \cdots, \|x’_n\|)\)
・ \(\vec{S}\) : saliency map
なお、 \(f’_j = exp(i \theta_j)\) としてsaliency map を求めるバージョンも存在しており、ほぼ同じsaliency map が得られることが知られています(参考文献③)。計算負荷的には、\(f’_j = exp(i \theta_j)\)の方が軽く、論文では、\(f’_j = r’_j exp(i \theta_j) (r’_j, \theta_j \in \mathbb{R})\) の方を用いています。
SR法を異常検知に適用する
上の手順で求めた saliency map に対してスコアを算出し、anomalyを判定します。具体的には、SRのスコアを \(\frac{S_i – \overline{S_i}}{\overline{S_i}}\) と定義し、この値が閾値\(\tau\) を超えた場合にanomalyと判定します。ここで\(S_i\) は \(x_i\) と同じ位置に対応する saliency map で、\(\overline{S_i} = \frac{1}{z}\sum_{j=1}^{z}{S_{i+1-j}}\) です。\(\tau\) はanomaly判定の閾値で、\(z\) はlocal average を算出する際に使用するデータ数です。
論文著者たちの工夫
詳しい方ならご存知のところですが、フーリエ変換はデータ端の影響を強く受けます。SR法でもデータ端の影響を受けてしまい、端のsaliency mapに意図しないピークが出る傾向があります。下の図は、左が時系列データで、右がそのデータにSR法を適用したものです。元々の時系列データでは特に異常がなかった端が、saliency map では両端の値が大きくなっているのがわかります。

saliency map のデータ端の意図しないピークのケアのために、著者たちは以下のように元々の時系列データに値を追加する工夫を行っています。\(\vec{x} \ = (x_1, x_2, \cdots, x_n)\)に対して、右端に\(\kappa\)個のデータを追加し、新しく\(\vec{\hat{x}}\ = (x_1, x_2, \cdots, x_n, x_{n+1}, \cdots, , x_{n+\kappa})\)を作成します。ここで、\(x_{n+1} = x_{n+2} = \cdots = x_{n+\kappa}\)で、算出式は以下です。
\(\overline{g}\ = \frac{1}{m}\sum_{i=1}^{m} g(x_n, x_{n-i})\)
\(x_{n+1} = x_{n-m+1} + \overline{g} \cdot m\)
ここで\(g(x_i, x_j)\)は傾きで、 \(g(x_i, x_j) = \frac{x_i – x_j}{i – j}\)です。
\(\vec{\hat{x}} \)に対して、saliency map: \(\vec{\hat{S}}\ = (\hat{S}_1, \hat{S}_2, \cdots, \hat{S}_n, \cdots, \hat{S}_{n+\kappa})\)を計算し、\((\hat{S}_1, \hat{S}_2, \cdots, \hat{S}_n)\)を取り出すと、データ補間を行わなかった場合よりもキレイなsaliency map を取得できることが実験的に明らかになっています。
SR法のデータへの適用例
上に示した時系列データに対して、SR法を用いてデータ補間を行わなかった場合(\(\kappa=0, m=0\))、データ補間を行なった場合(\(\kappa=5, m=5\))の2通りで、saliency mapとscore を算出した結果が下の図です。両者でその他のハイパーパラメーターは共通のものを用いており、\(\log{r’_i}\)を求める際のlocal average の幅 \(q\)は3, scoreを求める際のlocal average の幅 \(z\)は5としています。また、窓幅はデータ区間そのもの、つまり全データを含む幅としています。
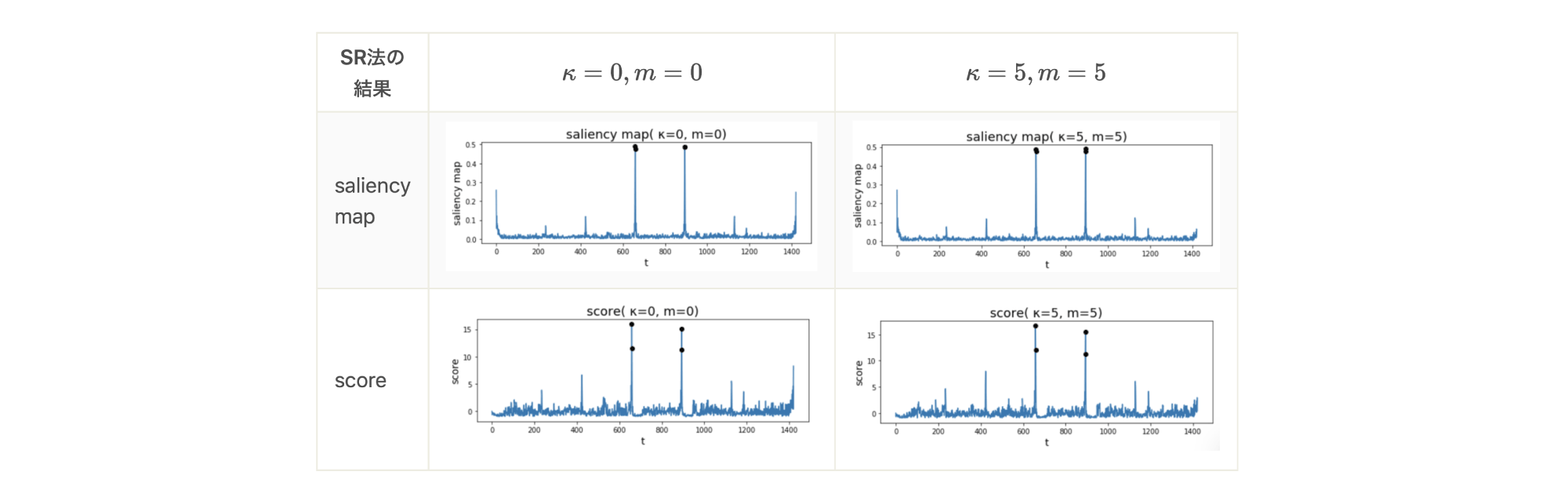
この図からわかることは、2点あります。
1. anomaly点に対して、saliency map、 score の値が大きくなっていて、anomalyを捉えることができている。
2. データ補間の有効性が確認できる。つまり、データ補間を行った\(\kappa=5, m=5\)では、saliency mapの右端の値のピークが消えている。それに付随する形で、scoreの右端のピークも消えている。
(※saliency mapの左端のピークを消したい場合は、データ補間を左端にも行えば良い。ただし、score を求める処理の性質上、scoreの左端のピークは消えるのでデータ補間を行う必要はない。)
いろいろなデータに対してのSR法の適用
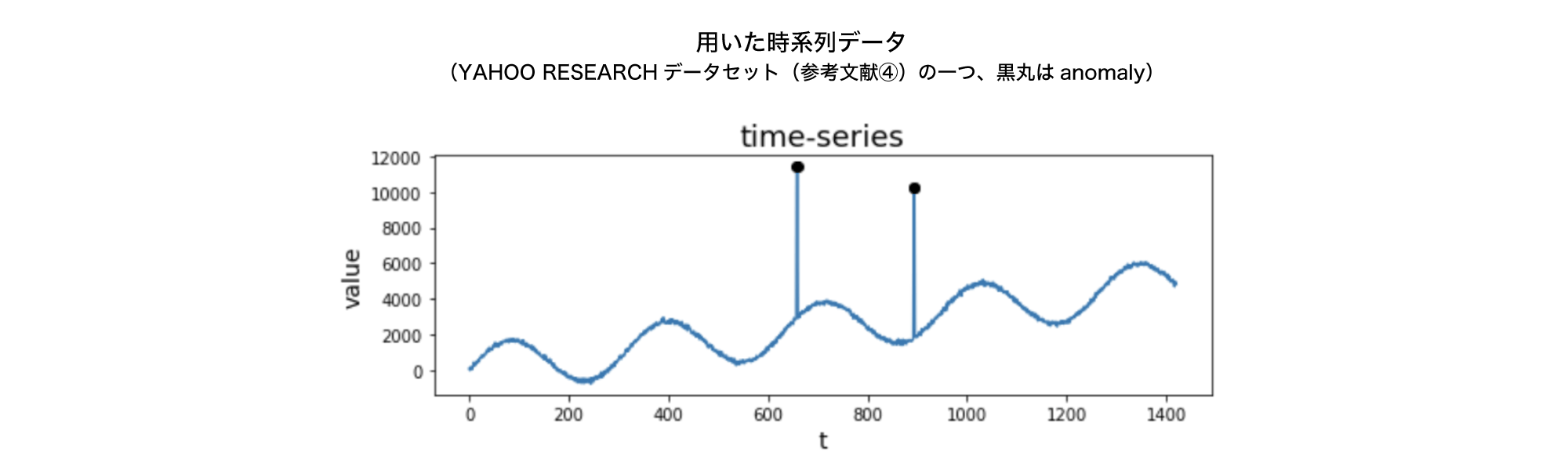
今回、YAHOO RESERCHの時系列異常検知用のデータセット(参考文献④) の全データに対してSR法の適用を試みました。その中からいくつか抜粋して、異常として検知できそうなデータにどのような傾向があるかを定性的に把握してみたいと思います。
下図の見方:各段の、
・左の図は、YAHOO データセットの時系列データで、黒丸がanomalyとして定義されたもの
・中央の図は、saliency mapデータ
・右の図は、saliency mapを求める際に\(f’_j = \exp(i \theta_j)\)としたバージョンでのsaliency map
右の図のsaliency mapの計算は、計算負荷の観点から軽量化したものですが、中央のものと大きく違わないことがわかります。
検知できるケース
・周辺の点に対して、飛び出しているケース
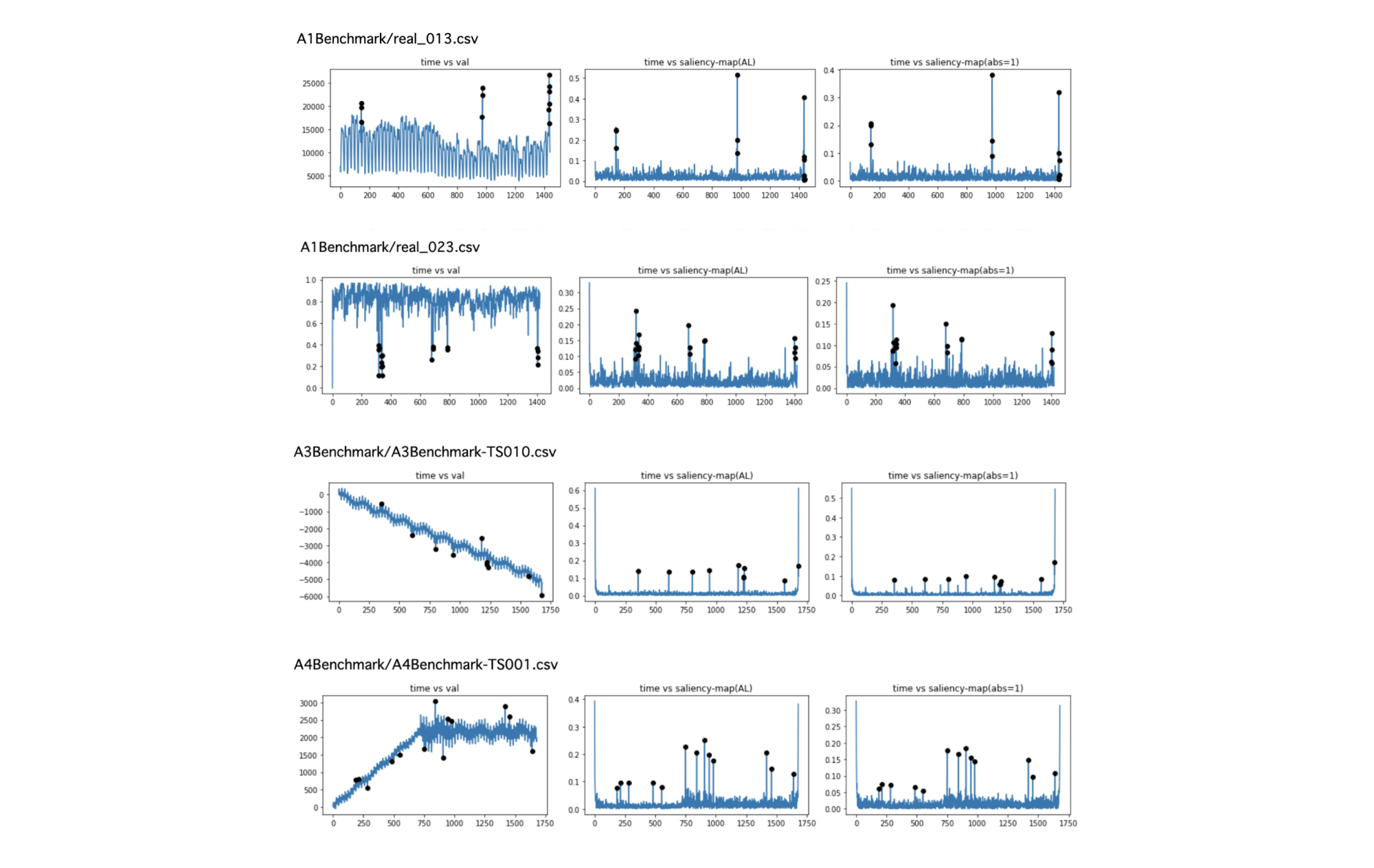
検知できないケース
・なだらかに変化しているような異常点や異常点が局在するケース


その他のケース
一方、目視では異常だと思えない異常点の検知がSR法だとできるケースもあります。

まとめ
今回は、時系列データからの特徴や異常を検出するための技術、時系列異常検知のうち、SR法を解説しました。
SR法は単一の閾値を用いていましたが、より柔軟な形で異常検出を行うことを目指したSR-CNNというモデルも開発されています。SR-CNNは、その名前の通り、SRにCNN(Convolutional Neural Network:畳み込みニューラルネットワーク)を組み合わせたモデルです。

SR-CNNにはチューニングの難しさなど、まだ課題が感じられる部分もあります。ですが、時系列異常検知の技術は、冒頭で紹介した気象データや株価、センサー領域などだけでなく、そのほか多くのビジネス領域での活用可能性をもつ技術です。今後ますますの改善と進歩が進み、様々なビジネスシーンで導入されていくことが期待されます。
参考文献
①Saliency detection: A spectral residual approach
②Time-Series Anomaly Detection Service at Microsoft
③Spatio-temporal saliency detection using phase spectrum of quaternion Fourier transform
④YAHOO RESEARCHデータセット A Benchmark Dataset for Time Series Anomaly Detection
コラム執筆者
機械学習エンジニア 大場 孝二
東京大学大学院 工学系研究科物理工学専攻 博士前期課程修了。修士(工学)。在学中は、物理の第一原理計算を用いて物質の性質の研究を行う。卒業後、証券会社のクオンツとして金利・為替系のデリバティブのプライシングモデルの作成・検証およびリスク計算業務を担当。その後、車両データを用いたデータ分析業務とサービス企画や仮説検証(PoC)に従事。2020年2月よりLaboro.AIに参画。